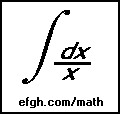The source-page: http://www.efgh.com/math/invcond.htm
Philip J. Erdelsky
9 Haziran 2001
Yaklaşık 32 yıl önce, bazılarının matris koşul numarasında “zarif sonuç” olarak tanımladığı şeyi yayınladım. Tekil olmayan bir matrisin, ancak ve ancak koşulsuz olması durumunda oldukça farklı yaklaşık sağ ve sol terslere sahip olduğunu belirtir. Ancak, bir kanıt yayınlamadım. Kanıt özellikle zor değil. İlk kez burada yayınlanmaktadır.
Aşağıdaki sonuçların tümü sonlu boyutlu gerçek vektör uzaylarıyla ilgilidir. Vektörler geleneksel olarak KOLON vektörleri ile temsil edilir. Tüm vektörler aynı boyuttadır ve tüm matrisler, vektörlerle aynı sayıda satıra sahip kare gerçek matrislerdir.
Sonlu boyutlu karmaşık vektör uzaylarının standart uzantıları vardır, ancak sonsuz boyutlu durumda bazı sonuçlar doğru değildir.
Tanım. Bir vektör normu gerçek değerli bir fonksiyondur ||x|| tüm x ve y vektörleri ve tüm skaler c için:
- ||x|| >= 0 eşitlikle ve ancak ve ancak x sıfır ise.
- ||cx|| = |c| ||x||.
- ||x + y|| <= ||x|| + ||y||.
Bir vektör normunun bir örneği Öklid normudur:
||x|| = sqrt(xT x).
Bir diğeri “maksimum norm”:
||x|| = max (|x1|, |x2|, …, |xn|),
burada x1, x2, …, xn x vektöründeki girişlerdir.
Tanım. Matris normu bir vektör normuna karşılık gelen gerçek değerli bir fonksiyondur ||A|| tarafından tanımlanan A matrisinin
||A|| = sup ||x|| = 1 ||Ax||.
Kompaktlık argümanları, üstünlüğün her zaman var olduğunu ve elde edildiğini gösterir; dolayısıyla her zaman en az bir sıfırdan farklı x vektörü vardır
||Ax|| = ||A|| ||x||.
Alternatif olarak ||A|| öyle bir sayı olarak tanımlanabilir ki
||Ax|| <= ||A|| ||x||,
tüm x için, en az bir sıfır olmayan x için eşitlikle. A ve B matrisler ve c bir skaler ise, bunu kanıtlamak oldukça kolaydır,
- ||A|| >= 0 eşitlikle ancak ve ancak, A = 0.
- ||cA|| = |c| ||A||.
- ||A + B|| <= ||A|| + ||B||.
- ||AB|| <= ||A|| ||B||.
Tanım. Durum sayısı, bir matris normuna göre bir tekil olmayan matris A
||A|| ||A-1||.
Yüksek bir koşul numarasına sahip bir matrisin kötü koşullu olduğu söylenir.
Aşağıdaki önermenin ispatı bazı konveksite teorisini gerektirir (Ek A’ya bakınız).
Önerme. Her vektör normu ve x ve y vektörlerinin her çifti için, x sıfır olmayan bir A matrisi vardır, öyle ki Ax = y ve ||A|| = ||y|| / ||x||.
Kanıt. Set {z | ||z|| <= ||x||} sınırlı ve dışbükeydir ve x sınırındadır. Bu nedenle, x bir destek hiperdüzlem (bazen teğet hiperdüzlem olarak adlandırılır) vardır. O zaman bir temel var
x, s2 , s3, …, sn,
x hariç tüm vektörlerin destek hiperdüzlemine paralel olduğu.
Şimdi, x y ve diğer tüm temel vektörleri sıfıra taşıyan doğrusal eşlemenin matrisi A olsun; yani, herhangi bir vektör w için
w = cx + c2s2 + c3s3 + … + cnsn,
Aw = cy.
O zaman c sıfır değilse,
w/c = x + (c2/c)s2 + (c3/c)s3 + … + (cn/c)sn.
w/c destek hiperdüzleminde olduğundan, kümenin sınırında veya dışında olmalıdır {z | ||z|| <= ||x||}. Buradan
||w/c|| >= ||x||,
||w|| >= |c| ||x||.
Buradan
||Aw|| / ||w|| = ||cy|| / ||w|| <= (|c| ||y||) / (|c| ||x||) = ||y|| / ||x||.
c = 0 ise, o zaman ||Aw|| = 0, yani eşitsizlik hala geçerli. Ayrıca, ne zaman eşitliğimiz var w = x. Buradan
||A|| = ||y|| / ||x||.
Teorem. A’nın tersine eşit olmayan herhangi bir tekil olmayan gerçek matris A ve herhangi bir gerçek matris B için,
||AB – I|| / ||BA – I|| <= ||A|| ||A-1||,
A tersine keyfi olarak yakın bir B matrisi için eşitlikle.
Ayrıca,
||BA – I|| / ||AB – I|| <= ||A|| ||A-1||,
A tersine keyfi olarak yakın bir B matrisi için eşitlikle.
Kanıt. İzin vermek D = BA – I. O zaman ilk iddia olur
||ADA-1|| / ||D|| <= ||A|| ||A-1||,
sıfır olmayan bazı D için eşitlikle. Sadece ölçeklendirerek D’yi keyfi olarak sıfıra yakın yapabiliriz.
Şimdi yukarıdaki (4) ile eşitsizliği kanıtlamak kolaydır. Eşitliğin geçerli olduğu bir D matrisinin varlığını kanıtlamak için, x ve y sıfırdan farklı vektörler olsun
||A-1x|| = ||A-1|| ||x||,
||Ay|| = ||A|| ||y||.
D öyle bir matris olsun ki
D(A-1x) = y,
||D|| = ||y|| / ||A-1x|| .
Sonra
||ADA-1|| ||x|| >= ||ADA-1x|| = ||Ay|| = ||A|| ||y|| = ||A|| ||A-1x|| ||D|| = ||A|| ||A-1|| ||x|| ||D||,
istenen sonucun hemen takip ettiği.
Ek A – Biraz Dışbükeylik Teorisi
Bu bölüm 30 Ekim 2006’da eklendi.
bir C ofℜn bir C alt kümesi (n-boyutlu gerçek vektör uzayı) C’deki her x ve y için, bunları birleştiren doğru parçası da C’deyse dışbükey denir, yani tx+ (1-t)y 0 ile 1 arasındaki her t için C’dedir.
Bir dışbükey kümenin iç ve kapanışının da dışbükey olduğu ve iki dışbükey kümenin arakesitinin dışbükey olduğu kolayca gösterilir.
ℜn m boyutlu bir simpleks, toplamı 1 olan negatif olmayan katsayılarla m+1 noktaları x0, x1, x2, … , xm (köşeler olarak adlandırılır) tüm doğrusal kombinasyonlarının kümesidir:
{a0x0 + a1x1 + a2x2 + … + amxm | a0 + a1 + a2 + … + am = 1, a0 >= 0, a1 >= 0, a2 >= 0, …, am >= 0},
ve burada x1-x0, x2-x0, … , xm-x0 vektörleri doğrusal olarak bağımsızdır.
Tek boyutlu tek yönlü bir çizgi parçası; iki boyutlu simpleks bir üçgendir ve üç boyutlu simpleks bir tetrahedrondur.
Bir dışbükey küme, bir simpleksin tüm köşelerini içeriyorsa, tek yönlünün her noktasını içerdiğini göstermek kolaydır.
Bir hiperdüzlem çevrilmiş (n-1)-boyutlu bir alt uzayıdır, yani, ℜn, de s, burada h hiperdüzlemde bir noktadır ve {h+s | s de S}, burada h hiperdüzlemde bir noktadır ve S, ℜn (n-1) boyutlu bir S alt uzayıdır. (Bu gösterim benzersiz değildir, çünkü h hiperdüzlem üzerinde herhangi bir nokta olabilir.) Hiperdüzlemin h’den geçen ve S’ye paralel olan hiperdüzlem olduğu söylenir. ℜ1 bir hiperdüzlem bir noktadır, ℜ2 bir hiperdüzlem bir düz çizgi ve ℜ3 bir hiperdüzlem bir düzlemdir.
Teorem A.1.. ℜn bir hiper ℜn iki parçaya; daha kesin olarak, hiperdüzlemin tümleyeni, hiperdüzlemin iki tarafı olarak adlandırılan iki ayrık açık kümeden oluşur. Ayrıca, bir taraftan diğerine bir doğru parçası hiper düzlemden geçer.
Kanıt. Hiperdüzlemin h’den geçtiğini ve S’ye paralel olduğunu varsayalım ve s1, s2, …, sn-1 S için bir temel ol. ℜn herhangi bir x için f(x), sütunları s1, s2, …, sn-1 ve xh olan matrisin determinantı olsun. O zaman f(x)=0 ise ve yalnızca x hiper düzlemdeyse. f sürekli olduğundan, iki küme {x ℜn | f(x) < 0} ve {x in ℜn | f(x) > 0} gerekli açık kümelerdir.
Ara değer teoremi diğer kısmı kanıtlamak için kullanılabilir.
Teorem A.2. ℜn boş olmayan bir dışbükey C kümesi ve C’nin dışında bir x noktası verildiğinde, C’yi x’ten ayıran bir hiperdüzlem vardır; yani, x ve C hiperdüzlemin zıt taraflarında bulunur.
Kanıt. C’nin kapanışında x’e en yakın bir c noktası düşünün (olağan Öklid metriğini kullanarak); standart kompaktlık argümanları, böyle bir noktanın olması gerektiğini gösterir. (Benzersiz olduğu da gösterilebilir, ancak bu ispat için teklik gerekli değildir.)
x, C’nin dışında olduğu için c, x farklıdır. Dolayısıyla, c ve x’i birleştiren doğru parçasına dik ℜn (n-1) boyutlu bir S alt uzayı vardır ve doğru parçasının orta noktasından geçen ve S paralel bir hiperdüzlem vardır.
x ve c noktaları hiperdüzlemin zıt taraflarındadır.
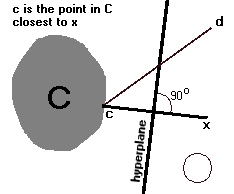
| Şimdi, çelişki amacıyla, hiper düzlemde veya x ile aynı tarafta C’de bir d noktası olduğunu varsayalım. C’nin kapanışı dışbükey olduğundan, d’den c’ye doğru parçası tamamen C’nin kapanışında yer alır. Ekteki çizim, d, c ve x’i içeren iki boyutlu bir düzlemdeki ilişkiyi gösterir. dcx açısı dardır, bu nedenle doğru parçası üzerinde c’ye yeterince yakın bir nokta, x’e c’den daha yakın olmalıdır, bu bir çelişkidir, çünkü c, C’nin x’e kapanışında en yakın noktaydı. |
|
Bir sonraki teorem, burada kullanılan türdeki dışbükey kümeler için açık olan, ancak aslında tüm dışbükey kümeler için doğru olan aşağıdaki önermeye dayanmaktadır.
ÖnermeA.3. S, ℜn‘de bir dışbükey küme olsun ve b, S’nin bir sınır noktası olsun. O zaman S’nin dışında, b’ye keyfi olarak yakın olan noktalar var.
Kanıt. Çelişki amacıyla, b’nin bazı komşularının S’nin dışında hiçbir nokta içermediğini varsayın. Dolayısıyla komşuluktaki her nokta, S’nin ya bir sınır noktası ya da bir iç noktasıdır.
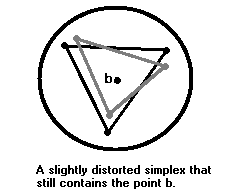
| Şimdi, içinde b ile komşuluğun içinde n-boyutlu bir simpleks oluşturun. Simpleksin köşeleri ya S’deki noktalar ya da S’nin sınır noktaları olmalıdır. Her iki durumda da, S’de bulunan, bunlara keyfi olarak yakın noktalar vardır. Hala b içeren hafif çarpık bir simpleks oluşturmak için bu tür noktaları seçin. |
|
S dışbükey olduğundan, çarpık tek yönlüdeki tüm noktaları içerir. Dolayısıyla b noktası S’nin bir iç noktasıdır. Bu istenen çelişkidir.
(1) hiperdüzlem sınır noktasını içeriyorsa ve (2) kümedeki hiperdüzlemde olmayan diğer tüm noktalar üzerinde yatıyorsa, bir hiperdüzlem tanjant hiperdüzlem veya bir sınır noktasında ℜn bir kümenin destek hiperdüzlemi olarak adlandırılır. hiper düzlemin bir tarafı.
Teorem A.4. ℜn kümesindeki bir dışbükey, her sınır noktasında en az bir teğet hiperdüzlemine sahiptir.
Kanıt. b bir dışbükey S kümesinin sınır noktası olsun x1, x21, … b’ye yaklaşan bir dış noktalar dizisi olsun. Teorem A.3 göre her xi için b’yi S’den ayıran bir hiperdüzlem Hi. Bu hiperdüzlemlerin bazı alt dizileri istenen teğet hiperdüzlemine yakınsar.
Hiper düzlemlerin nasıl birleşebileceğini sorabilirsiniz. Sadece Hi xi S’nin kapanışındaki en yakın noktaya ve onun alt uzayı S için normalleştirilmiş bir tabana birleştiren doğruyu kestiği nokta ile ilişkilendirin. Tüm bu vektörlerin koordinatları sınırlıdır, dolayısıyla hepsinin yakınsak altdizileri vardır.