The source-page: http://www.math.stonybrook.edu/~tony/mazes/satmaze.html
Labirentlerden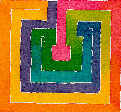
Matematiğe
Bu labirentlerden en bilineni Girit labirentidir. Oyun olarak çizilebilir.
İşte başka bir örnek. Bu labirent, birkaç ortaçağ İbranice el yazmasında görülür. Bu labirent Girit labirentine yüzeysel bir benzerlik gösterse de, yakından bir karşılaştırma oldukça farklı olduklarını gösterir. Jericho labirentinde 7 seviye bulunurken Girit labirentinde 8 seviye bulunur ve seviyelerin ulaşıldığı sıra bir labirentten diğerine farklılık gösterir. Her iki labirentte de yol doğrudan 3. seviyeye gider (dışarıyı 0 olarak sayar), ancak Girit labirentinde 2. ve 1. seviyelerden ikiye katlanırken, Jericho labirentinde 2. ve 5. seviyeye dönmeden önce 4. ve 5. seviyelerde devam eder. 1. tam seviye sekansları olan
Girit 032147658
Jericho 03452167.
Bu iki labirentin paylaştığı ve basit bir matematiksel tanımla bir labirent sınıfını tanımlamaya hizmet edecek özellikler, bunlara basit, dönüşümlü, geçiş labirentleri (b.a.t. labirentleri) olarak adlandırılarak özetlenebilir.
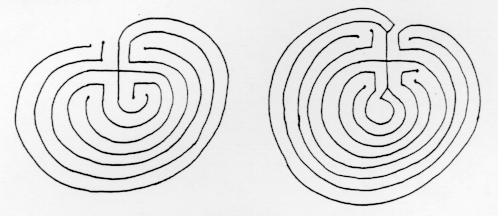TRANSİT labirentleri çünkü yol labirentin dışından merkeze çatallanma olmadan ilerliyor. Örneğin bu labirentler transit labirentler değiller: birinde yol girdiği aynı tarafta çıkıyor; diğerinde ise labirent koşucusunun hangi yolu seçeceğini seçmesi gereken noktalar var.
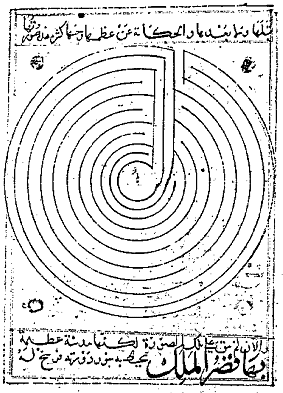ALTERNATİF çünkü labirentin planı belirli sayıda eşmerkezli veya paralel seviye üzerine yerleştirilmiştir ve labirent yolu seviye değiştirdiğinde yön değiştirir. Örneğin bu labirent, bir ortaçağ Arap coğrafya kitabında Konstantinopolis’in planını temsil eden, farklı seviyelere sahiptir, ancak yön değiştirmeden 10. seviyeden 1. seviyeye spiraller çizdiği için dönüşümlü değildir. Seviye dizisi 0.3.4.5.6.7.8.9.10.1.2.11, göreceğimiz gibi, değişen bir labirentin seviye dizisi olarak gerçekleşemez.
BASİT çünkü yol esasen her düzeyde tam bir daire oluşturur; özellikle her seviyede tam olarak bir kez seyahat eder. Örneğin, Chartres’te (burada gösterilmektedir) ve diğer birkaç katedralde bir kaldırım labirenti olarak ortaya çıkan ve Lucca’daki Katedral’de bir sütuna oyulmuş bu alternatif geçiş labirenti basit değildir: yolun dört farklı noktası vardır. seviyeleri değiştirebilir. Bu labirent deseni, Girit tasarımının ve onun Romalı soyundan gelenlerin bir Hıristiyan detaylandırması ve büyütülmesi olarak ortaya çıkmış gibi görünüyor; Theseus miti ile ilişki devam etti. Yeni tasarımın kendisi oldukça kalıcıydı. 9. yüzyıldan kalma ortaçağ el yazmalarında görülür; Chartres katedrali 1200 yılı civarında inşa edilmiştir; ve 16. yüzyılın başlarında, aynı desen bir floransali kasson üzerine boyanmıştır. Şimdi, merkezde Minotaur ile savaşan zırhlı bir Theseus ile 3 boyutlu olarak işleniyor.
Basit, değişken bir geçiş labirentinin TOPOLOJİSİ, tamamen seviye dizisi ile belirlenir.
Tony Phillips
Matematik Bölümü New York Eyalet Üniversitesi Stony Brook
tony at math.stonybrook.edu
30 Eylül 2020