The source-page: http://www.efgh.com/math/pi.htm
Philip J. Erdelsky
26 Temmuz 2001
Matematik birçok ilginç aşkın sabit içerir, ancak bunlardan sadece biri eskiler tarafından biliniyordu. Bu ise π, bir dairenin çapına çevresi oranına sahiptir.
Arşimet, π için yaklaşık bir değer hesaplayan ilk matematikçiydi. Önceki değerler, sınırlı doğrulukta fiziksel ölçümlere dayanıyordu.
Sadece Arşimet tarafından bilinen matematiği kullanarak yaklaşık bir π değeri hesaplamak için Arşimet yöntemini kullanacağız. Ancak hesaplamalarımızı bir bilgisayarda yapacağız ve onun yaptığından çok daha doğru bir değer elde edeceğiz.
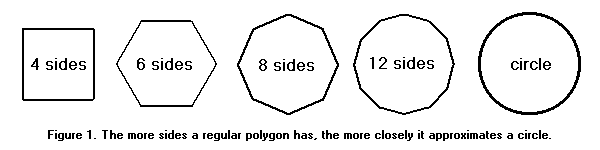
Eskilerin çok iyi bir limit teorisi yoktu; matematikçi olmayanların çoğu da öyle. Ama bazı şeyler oldukça açık. Birçok kenarı olan düzgün bir çokgen yaklaşık olarak bir dairedir. Çevresi yaklaşık olarak dairenin çevresidir ve alanı yaklaşık olarak dairenin alanıdır. Çokgenin ne kadar çok kenarı varsa, yaklaşım o kadar doğru olur. Çokgenin yeterli kenarı varsa, istenen herhangi bir doğruluk derecesi elde edilebilir.
π için yaklaşık bir değer bulmak için yarıçapı 1 olan bir daireye düzgün çokgenler yazacağız. Bazı durumlarda çokgenlerin çevreleri, Arşimet tarafından bilinen Pisagor teoreminden daha gelişmiş bir şey kullanılarak hesaplanabilir. Özellikle, n kenarlı düzgün çokgenin her bir kenarının uzunluğunu biliyorsak, 2n kenarlı düzgün çokgenin her bir kenarının uzunluğunu hesaplayabiliriz.
Şekil 2’de, izin AB biri N kısımda yer alan bir daire içinde yer muntazam bir çokgenin kenarlarına göre O, uzun ve bir yarıçap, bir birim. AB‘nin uzunluğu s olsun.
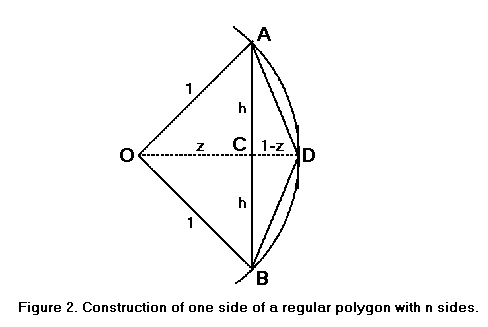
AOB açısının açıortayı OCD olsun. O halde AOC ve BOC üçgenleri uyumludur; dolayısıyla C‘deki açılar dik açılardır ve AC = CB. Öyleyse,
- h = s/2
- z = √(1-h2)
Çokgenin çevresi ns ve dairenin çapı 2. Bu nedenle yaklaşık değeri π olan ns/2.
AD ve BD doğru parçaları, kenarları 2n olan yazılı bir çokgenin kenarlarıdır. Her birinin uzunluğu
- √(h2 + (1-z)2))
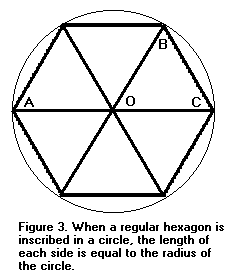
n = 6 olduğu durumda, s = 1 olduğunu biliyoruz. Bu bilinen bir gerçektir, ancak kısa bir kanıt vereceğiz. Altıgen düzgün olduğundan, merkezdeki altı açı da eşittir. ACB açısı bir daire içinde çizilir, bu nedenle, altı açıdan ikisine eşit olan, kesişen AOB açısının yarısıdır. Dolayısıyla ACB açısı BOC açısına eşittir. OB ve BC karşılıklı kenarları da eşittir. Benzer argümanlar, diğer her kenarın dairenin yarıçapı kadar uzun olduğunu gösterir.
Tek yapmamız gereken, n = 12, 24, 48, 96, vb. için değerleri elde etmek için bu formülü tekrar tekrar uygulamaktır.
Aşağıdaki C++ programı gibi basit bir bilgisayar programı bu hesaplamaları hızlı bir şekilde yapacaktır.
#include <stdio.h>
#include <math.h>
void main(void)
{
double s = 1.0;
double n = 6.0;
puts("number of sides approximate value of pi");
while (n < 500000000.0)
{
printf ("%9.0f %18.16f\n", n, n*s/2.0);
double h = s / 2.0;
double z = sqrt(1.0 - h * h);
s = sqrt(h * h + (1.0 - z) * (1.0 - z));
n *= 2;
}
}
Sonuçlar şöyle görünür:
number of sides approximate value of pi
6 3.0000000000000000
12 3.1058285412302489
24 3.1326286132812378
48 3.1393502030468667
96 3.1410319508905098
192 3.1414524722854624
384 3.1415576079118579
768 3.1415838921483186
1536 3.1415904632280505
3072 3.1415921059992717
6144 3.1415925166921577
12288 3.1415926193653840
24576 3.1415926450336911
49152 3.1415926514507682
98304 3.1415926530550373
196608 3.1415926534561045
393216 3.1415926535563719
786432 3.1415926535814380
1572864 3.1415926535877046
3145728 3.1415926535892713
6291456 3.1415926535896630
12582912 3.1415926535897611
25165824 3.1415926535897856
50331648 3.1415926535897913
100663296 3.1415926535897931
201326592 3.1415926535897931
402653184 3.1415926535897931
Hesaplamak için bir abaküsten daha iyi bir şeyi olmayan Arşimet, 96 kenarda durmak zorunda kaldı.